A Markov Blanket is the smallest “information shield” you need around a variable (or a system) so that everything outside the shield becomes irrelevant once you know what is inside it. Formally, it is a set of variables that renders a target variable conditionally independent of all other variables in the model, meaning the blanket contains all the information you need for inference about the target - wikipedia ![]()
In a Bayesian Network, the Markov blanket of a node has a pleasantly concrete shape: the node’s parents, its children, and the other parents of its children (often called its “spouses”). Condition on those, and the rest of the network stops mattering for predicting that node.
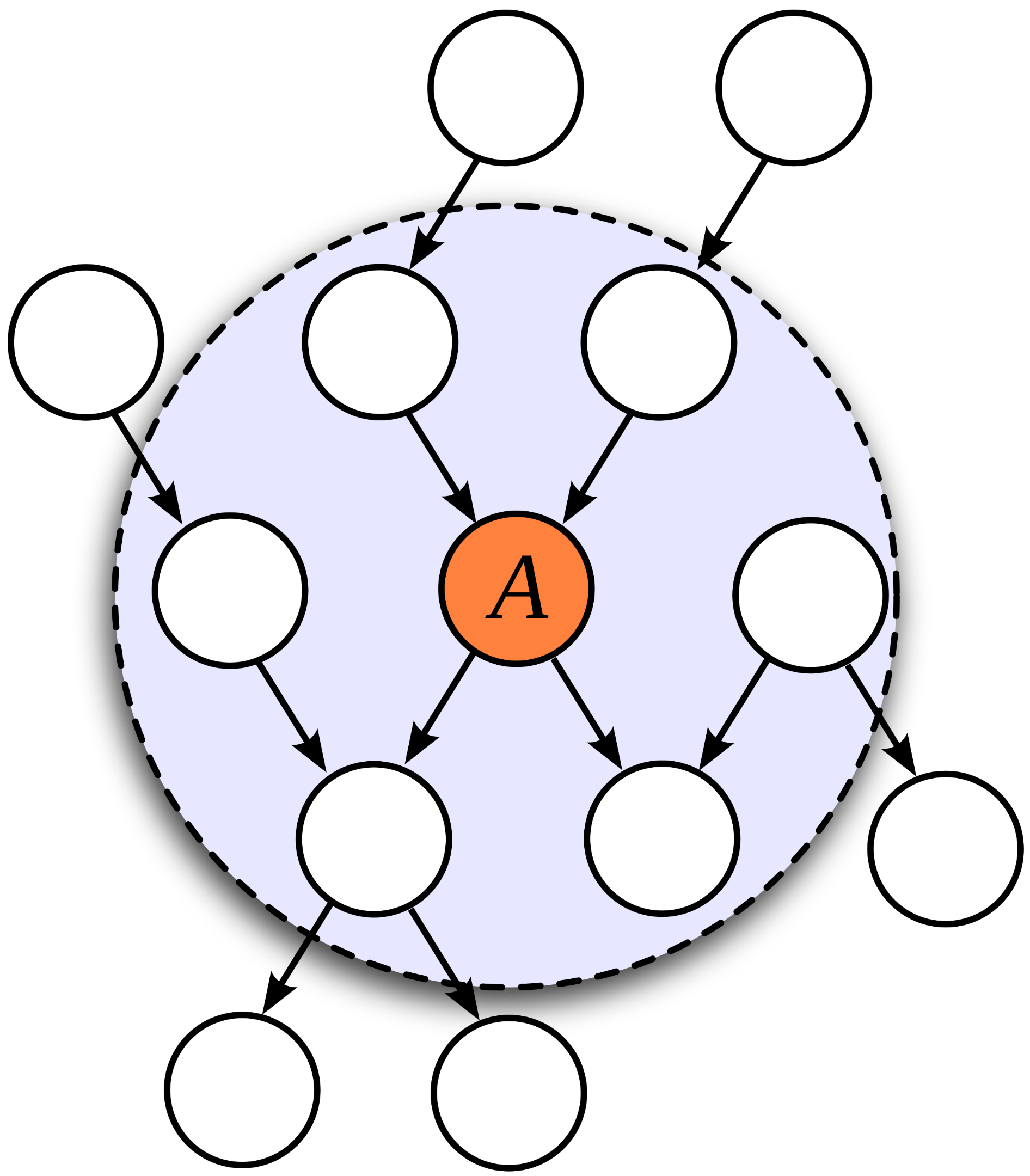
In a Bayesian network, the Markov Boundary of node A includes its parents, children and the other parents of all of its children - wikipedia ![]()
The term Markov blanket (and the related idea of a minimal “Markov boundary”) is commonly credited to Judea Pearl’s work on probabilistic reasoning and graphical models, where the point is pragmatic as much as philosophical: if you can identify the blanket, you can do efficient reasoning without carrying the whole universe in your head.
This makes Markov blankets useful in Feature Selection. If you are trying to predict Y from many candidate variables, the blanket tells you which variables are sufficient, and which are redundant once the blanket is known. In practice, people hunt for approximate blankets because real data is messy, causal structure is uncertain, and different blankets can appear when the system is degenerate or the data is limited.
In Karl Friston’s Free Energy Principle and Active Inference, Markov blanket is lifted from a graph-theoretic tool into a general way of talking about boundaries between a system and its environment.
The claim is not that a blanket must be a physical membrane, but that a boundary can be defined statistically: internal and external states are conditionally independent given the states on the blanket (often described as sensory and active states). This is used to formalise how something can be distinct, persist over time, and interact with its surroundings without needing to model everything everywhere - - [https://arxiv.org/abs/1906.10184 arxiv.org ![]() - pmc.ncbi.nlm.nih.gov
- pmc.ncbi.nlm.nih.gov ![]()
A helpful intuition is to treat the blanket as a “surface of contact”. Inside the blanket are internal variables you want to protect or summarise. Outside are external variables you do not directly control. On the blanket are the variables through which the two sides couple. When you choose the blanket well, you get a clean separation: you can reason locally while still being embedded in a larger world.
The big caution is that “blanket” can mean different things in different contexts. In Bayesian networks it is a structural set of nodes in a graph. In Friston-style discussions it can be used as a more general partition in dynamical systems. The shared heart of the idea is conditional independence and the computational gift it gives: you can focus on the boundary variables instead of the whole cosmos - royalsocietypublishing.org ![]()
# See - Bayesian Network and Conditional Independence. - Markov Boundary and Feature Selection. - Causality and Causal Markov Condition. - Free Energy Principle and Active Inference. - Graphical Model and d-separation.